[CS231n 2017] Lecture4 Intro to NN
2020년 딥러닝을 처음 접한 시기에 스탠포드 cs231n 2017 강의를 들으며 정리한 내용을 옮겨놓은 내용입니다.
이해한 내용에 부정확한 부분이 있을 수 있습니다. (정정 댓글 환영합니다.)
Intro to NN
Backpropagation (엄청 중요!)
Computational Graphs

함수를 computational graph 를 통해 표현하게 됨으로써 backpropagation 이라는 것을 사용할 수 있게 되었다.
일단 첫 번째 설명
backpropagation은 gradient를 얻기 위해 computational grapah 내부의 모든 변수에 대해 chain rule을 재귀적으로 사용한다.
예시 : f(x,y,y) = (x+y)z
x,y,z 의 gradient 를 알고자 하는 것!
뒤에서부터 시작
결과값, z, q, y, x 에 대하여 계산

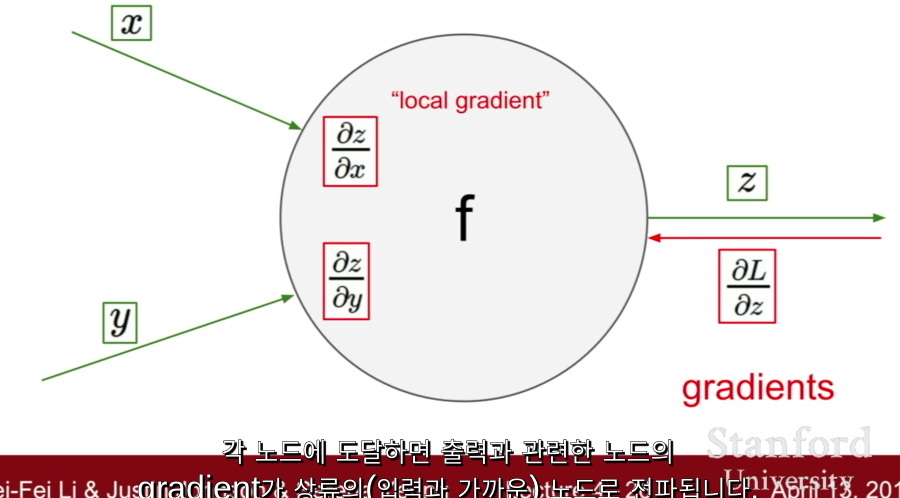
그렇다면, backpropagation 으로 인해 하나의 param 단위로 모든 계산이 다 끊어질 수 있게 되는건가??
upstream gradient 와 local gradient로 계속 계산하는 것
⇒ local gradient & upstream gradient
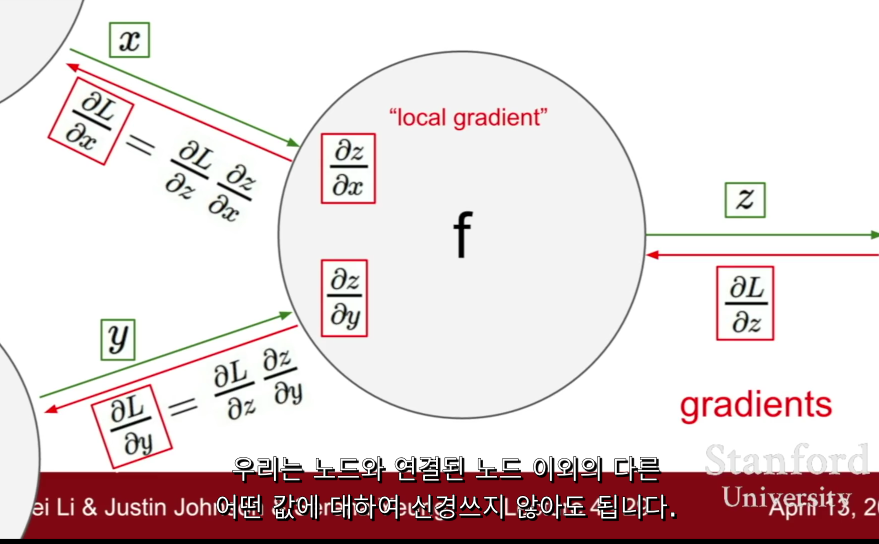
computational graph 의 관점에서 backpropagation, chain rule 을 통해 gradient를 계산할 수 있다.
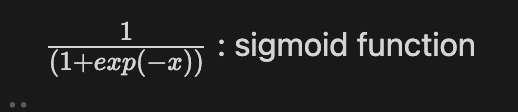
node 를 sigmoid gate로 나타내기

w0,x0 을 보면,
upstream gradient 는 0.2임
근데, upstream gradient * local gradient 를 했더니 -0.2 라는 값이 내려오잖아.
그러니까 w0 에 대한 gradient 는 1인거임.
같은 원리로, x0 은 0.4라는 값이 내려오잖아.
x0에 대한 gradient 가 2라는 소리지.
⇒ 아닌거같음!
⇒ 다시... w0와 x0에 대해 upstream gradient 가 0.2임! 그리고 local gradient(초록색값) 는 w0는 2, x0은 -1임. 그래서, 각각의 gradient를 구해보면 x0 : 2*0.2 = 0.4 , w0 : -1 * 0.2 = -0.2 이렇게 나오는거임!
Patterns in backward flow
- add gate : gradient distributor
- max gate : gradient router
- mul gate : gradient switcher
여기까지 스칼라 값에 대한 이야기를 했는데, 이제 벡터 값에 대한 이야기를 해봅시다.
Gradients for vectorized code
jacobian 행렬이 대각선 형태인 이유
요소별이기 때문에, 입력의 각 요소는 오직 상응하는 출력 요소에만 영향을 주게 되어이씩 때문에.
gradient 벡터는 항상 원본 벡터와 사이즈가 같다.
각 gradient (각 element) 는 함수의 최종 출력에 얼마나 영향을 끼치는지를 나타내는 것.

⇒ gradient 계산 이후 모양을 비교해보는 것이 좋다. ( gradient 벡터와 원본 벡터의 사이즈 동일성 확인 )
⇒ 마지막 출력에 대한 gradient는 1 (항상 첫 단계)
⇒ L2 이전의 중간 변수인 q에 대한 gradient를 찾기 원한다. q는 2차원 벡터.
⇒ 궁극적으로 q의 각각의 요소가 f의 최종값에 어떤 영향을 미치는지가 궁금한 것.
⇒ f를 q에 대해 편미분함으로써 공식을 얻고, 대입하여 gradient를 구한다!
W의 gradient를 구하는 것은
x초록의 0.2*초록끼리 계산하면 W gradient의 1행이 나온다.
x초록의 0.4*초록끼리 계산하면 W gradient의 2행이 나온다.
forward pass, backward pass
forward pass 에서는 노드의 출력을 계산하는 함수를 구현하고
backward pass 에서는 gradient를 계산한다.
forward pass의 값(연산 결과)은 이후에 backward pass에서 자주 사용하기에 저장해야한다.
Example : Caffe layers
computational node 의 목록을 볼 수 있다.
그리고 여기에 모두 결론적으로 forward pass, backward pass 가 있는거임.
정리!
- computational graph ⇒ 출력으로 이어지는 계산이 무엇인지 파악
- 계산에 필요한 중간 변수에 대한 gradient를 가져온다.
- chain rule 을 이용하여 연결한다.
computational graph 에 chain rule 을 재귀적으로 적용하는 것.
Neural Networks
linear layer 를 지속적으로 쌓는다면, 결국 선형 함수가 되어버리는 것.
그래서 비선형 layer(함수)가 필요하다.

광범위하게 이야기하면, 신경망은 함수들의 집합(class)
비선형의 복잡한 함수를 만들기 위해서 간단한 함수들을 계층적으로 여러개 쌓아올린 것.
W1의 입력과 직접적으로 연결되어 있어 나타나는 것이고, w2는 h의 스코어가 된다.
h는 값이다. h는 w1에서 가지고 있는 템플릿에 대한 점수.
⇒ w1의 각 템플릿이 얼마나 많은지를 나타내주는 것이고 w2는 이들 모두에 가중치를 부여하고 모든 중간중간 점수를 더해 클래스에 대한 최종 점수를 얻는 것.
w2는 이들 모두에 가중치를 부여하고 모든 중간 점수를 더해 클래스에 대한 최종 점수를 얻는 것
h 이전에 비선형성이 발생하기 때문에 h는 비선형 값이다.
여러 layer 를 쌓는 아이디어에서 deep neural network 라는 개념이 나온 것.

신경망 아이디어
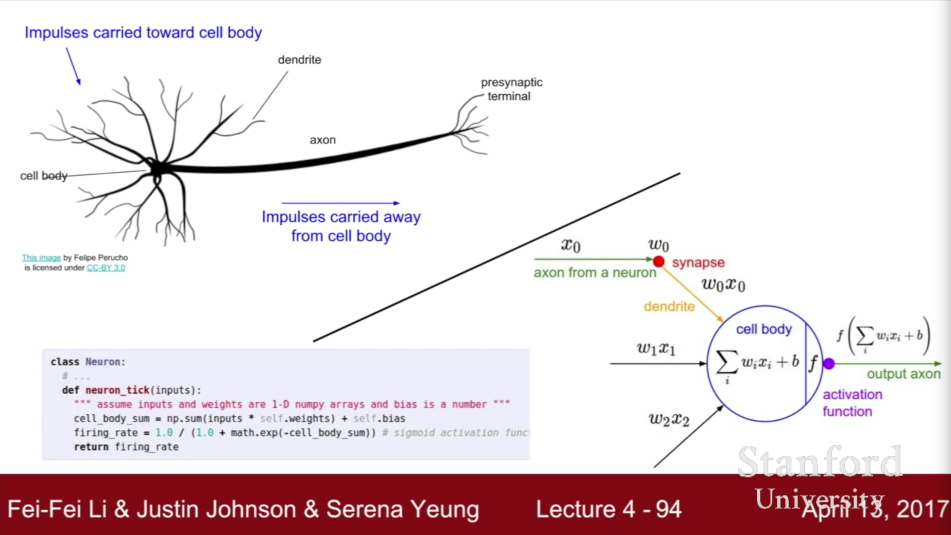
ReLU : 뉴런의 행동과 가장 비슷한 activation function
실제 생물학적 신경망은 엄청 복잡하기 때문에, 모델을 만드는 것에 주의가 필요한 부분들이 있다.
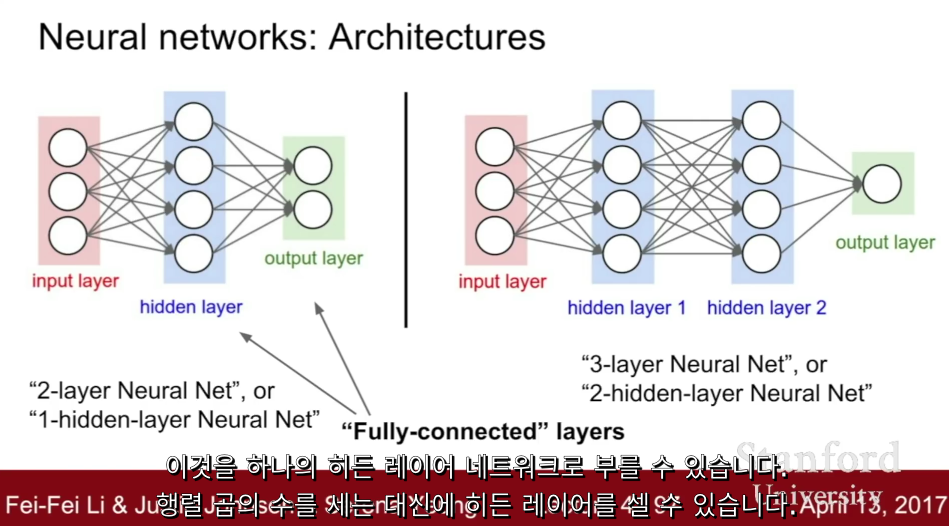

참고 설명
우리가 가지고 있는 벡터 행렬 형태의 출력은 비선형성을 가진다. 여기서 사용한 F는 Sigmoid 함수이다. 데이터는 x로 받고 첫 번째 행렬 곱 w1은 가장 윗줄에 있다. 비선형성을 적용한 다음, 두 번째 히든 레이어 h2를 얻기 위한 두 번째 행렬곱을 한다. 그리고 최종 출력을 얻는다.
'AI > cs231n' 카테고리의 다른 글
| [CS231n 2017] Lecture7 TNN 2 (0) | 2022.08.28 |
|---|---|
| [CS231n 2017] Lecture6 TNN 1 (0) | 2022.08.28 |
| [CS231n 2017] Lecture5 CNN (0) | 2022.08.28 |
| [CS231n 2017] Lecture3 Loss functions and Optimization (0) | 2022.08.27 |
| [CS231n 2017] Lecture2 Image Classification (0) | 2022.08.27 |